Un recipiente de aluminio de 300g contiene 200g de agua a 10º C. Si se vierten 100 g más de agua, pero a 100º C, calcular la temperatura final de equilibrio del sistema. R: 34.6º C.
Se ha encontrado que la temperatura de un gas es una medida de la energía cinética promedio de traslación del centro de masa de las moléculas del gas, sin considerar la energía asociada al movimiento de rotación o de vibración de la molécula respecto al centro de masa. Esto es así, porque en el modelo simple de la teoría cinética se supone que la molécula es sin estructura.
De acuerdo a esto, se analizará el caso simple de un gas ideal monoatómico, es decir, de un gas que tiene un átomo por molécula, como el helio, neón o argón. Cuando se agrega energía a un gas monoatómico contenido en un envase de volumen fijo (por ejemplo calentando el envase), toda la energía agregada se ocupa en aumentar la energía cinética de traslación de los átomos. No existe otra forma de almacenar la energía en un gas monoatómico. De la ecuación 12.20, se tiene que la energía interna total U de N moléculas (o n moles) de un gas ideal monoatómico se puede calcular de:
De esta ecuación se deduce que para un gas ideal, U es función sólo de la temperatura T. Si se transfiere calor al sistema a volumen constante, el trabajo realizado por el sistema es cero, esto es, W = 0. Por la primera ley de la termodinámica, se obtiene:
Esto significa que todo el calor transferido se ocupa en aumentar la energía interna (y la temperatura) del sistema. En la figura 13.10 se describe el proceso a volumen constante desde i hasta f1, donde ΔT es la diferencia de temperatura entre las dos isotermas.
Reemplazando el valor de Q dado por la ecuación 13.1, con C = nc, se obtiene:
donde cV es la capacidad calórica molar del gas a volumen constante, válida para todos los gases monoatómicos.
El cambio de energía interna para un gas ideal, en un proceso a volumen constante, se puede expresar como:
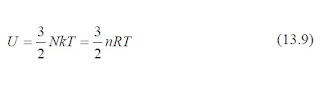
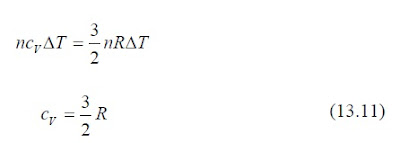
Comentarios
Publicar un comentario