CAPACIDAD CALORICA DE UN GAS IDEAL Paso 1

Suponga ahora que el gas se lleva por un proceso termodinámico isobárico, desde i hasta f2, como se muestra en la figura 13.10. En esta trayectoria, la temperatura aumentó en la cantidad ΔT. El calor que se debe transferir al gas en este proceso está dado por Q = n cP ΔT, donde cP es la capacidad calórica molar a presión constante. Como el volumen aumenta en este proceso, se tiene que el trabajo realizado por el gas es W = P ΔV, y aplicando la primera ley de la termodinámica, se obtiene:

En este caso el calor agregado al gas se usa en dos formas: una parte para realizar trabajo externo, por ejemplo para mover el émbolo del envase y otra parte para aumentar la energía interna del gas. Pero el cambio de energía interna para el proceso de i hasta f2 es igual en el proceso de i hasta f1, ya que U para un gas ideal dependen sólo de la temperatura y ΔT es la misma el cada proceso. Además como PV = nRT, para un proceso de presión constante se tiene que PΔV = nRΔT. Reemplazando en la ecuación 14.5, con ΔU = n cV ΔT, se obtiene:

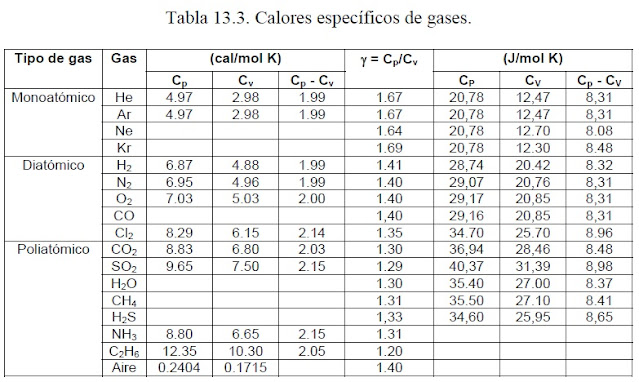
Esta expresión que se aplica a cualquier gas ideal, indica que la capacidad calórica molar a presión constante es mayor que la capacidad calórica molar a volumen constante por una cantidad R, la constante universal de los gases. Como para un gas monoatómico cV = (3/2)R = 12.5 J/molK, el valor de cP es cP = (5/2)R = 20.8 J/molK. La razón de estas capacidades calóricas es una cantidad adimensional llamada gamma, γ, de valor:

Los valores de cP y γ concuerdan bastante bien con los valores experimentales para los gases monoatómicos, pero pueden ser muy diferentes para gases más complejos, como se puede observar en la tabla 13.3, donde se listan valores de la capacidad calórica molar para algunos gases. Esto no debe sorprender ya que el valor de cV fue determinado para gases ideales monoatómicos y se espera una contribución adicional al calor específico debido a la estructura interna de las moléculas más complejas.

La diferencia de valor entre cV y cP es consecuencia del hecho de que en los procesos a volumen constante, no se realiza trabajo y todo el calor se usa para aumentar la energía interna (y la temperatura) del gas, mientras que en un proceso a presión constante, parte de la energía calórica se transforma en trabajo realizado por el gas. En el caso de sólidos y líquidos calentados a presión constante, se realiza muy poco trabajo debido a que la dilatación térmica es pequeña (ver ejemplo 13.10). En consecuencia, cV y cP son aproximadamente iguales para sólidos y líquidos.

Comentarios

Entradas más populares de este blog

Conducción radial de calor a través de una esfera hueca

Además del problema de la pared plana, hay otros dos problemas básicos unidimensionales de estado estacionario que consideramos: Dichos problemas son el caso de un cilindro hueco tan largo que las pérdidas en los extremos son desperciables, o bien que sus extremos se encuentran aisladas para evitar pérdida y, además, el caso de una esfera hueca. En ambos problemas, se mantiene constante la temperatura de las superficies interior y exterior. En primer lugar, considere la esfera hueca, como se aprecia en esta figura. Atacamos este problema haciendo un balance de energía en un elemento diferencial de volumen, con el fin de determinar la ecuación diferencial apropiada. Observando que la conducción térmica es constante, que existen condiciones de estado estacionario y que no hay fuentes de calor, escribimos el balance de energía:

Leer mas »

Problema Radio Critico de Aislamiento

A través de una tubería de 3 pulgadas de diámetro exterior circula vapor húmedo a 325°F, la tubería esta aislada con asbesto. El coeficiente convectivo de transferencia de calor entre la superficie exterior del asbesto y el aire que lo rodea a 70°F es igual a 0.5 Btu/h-pie²°F. Determine el radio critico de aislamiento Dado este valor de r2, calcule la pérdida de calor por pie en la tubería, y la temperatura de la superficie exterior. Solución Comentarios: Se debe notar, de la parte (2), que para valores r2 diferentes rcr, los valores de Q/L serán menores. Los resultados de la parte (3) muestran que se debería agregar más aislante para evitar perjuicios humanos. Puesto que más aislante también reduce de valor a Q/L, se desperdiciará menos energía durante la operación de la tubería de vapor, y el único costo extra será el de la inversión inicial en el aislante.

Leer mas »

Ejemplo 2: CAPACIDAD CALORICA Y CALOR ESPECIFICO

Un trozo de metal de 50 g que se encuentra a 200º C se sumerge en un envase que contiene 0.4 kg de agua inicialmente a 20º C. Si la temperatura final de equilibrio del sistema mezclado es 22.4º C, calcular: a) el calor específico del material, b) el calor ganado por el agua. Despreciar la transferencia de calor al envase y al medio ambiente. Solución: los datos son cA=4186 J/kgºC, mm = 50g, Tim = 200ºC, mA = 400g, TiA = 20ºC, Tfm=22.4ºC =TfA. a) Al introducir el metal caliente en el agua mas fría, el metal se enfría y el agua se calienta, alcanzando ambos 22.4º C, es decir, el metal pierde calor y el agua gana calor.

Leer mas »

Problema Paredes Compuestas

Una pared de una casa mide 8 pies por 20 pies, no tiene ventanas, y consta de 1/4 de pulgada de forro de tela de roble y 2 pulgadas de pino blanco. La temperatura interna de la pared es de 70F y la temperatura externa en la pared es de 10F. Determine la pérdida de calor a través de la pared en Btu/h. Solución Datos: Una pared sin ventanas tiene un diferencial de temperaturas entre sus superficies interior y exterior. 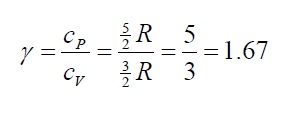Comentarios: La pérdida total en la conducción de calor a través de la pared hecha con roble pino es de 3450 Btu/h.

Leer mas »

Sistemas con resistencia interna despreciable (I)

La clase de problemas transitorios que mejor se presentan para ser analizados son aquellos que tienen una resistencia interna al flujo de calor despreciable. En dichos problemas, la resistencia conectiva en la frontera del sistema es muy grande, comparada con la resistencia interna debida a la conducción. En esencia, el sólido se comporta como si tuviera una conductividad térmica infinita en el sentido de que la temperatura es siempre uniforme a través de todo el sólido y varias únicamente con el tiempo. En la realidad, nunca es posible conseguir con precisión dicha situación, ya que todos los materiales tienen una conductividad térmica finita y, al agregar o quitar calor, deben existir gradientes de temperatura según lo demuestra la ley de conducción de calor de Fourier, Q = -kA(δT/δn). Sin embargo, cuando la resistencia convectiva en la frontera del sólido es grande, comparada con la resistencia interna debido a la conducción, la parte principal de la variación de temperatura espacia...

Leer mas »

Conducción de calor a través de una pared plana Problema 1

Se modela un horno casero de modo que resulte en forma de caja rectangular, hueca, con dimensiones interiores de 46 cm x 61 cm x 76 cm y exteriores de 51 cm x 66 cm x 81 cm. Si se ignoran las pérdidas de calor a través de las esquinas y las aristas, la tempertura de la pared interior es de 204°C, la temperatura de la pared exterior es de 38°C, y el material de la pared es asbesto, estime la potencia en watts que se suministra, necesaria para mantener esta condición de estado estacionario. Solución: Datos: Hay tres parejas de paredes de un horno casero a través de las cuales puede ocurrir transferencia de calor por conducción.

Leer mas »

Conducción bidimensional bajo condiciones de estado estacionario (I)

En los anteriores post analizamos la conducción de calor unidimensional , bajo condiciones de estado estacionario, en paredes planas, cilindros, y esferas. En muchas aplicaciones de ingeniería, pueden variar las temperaturas en un cuerpo dado en dos o tres direcciones de coordenadas, y por esto se hace necesario discutir la conducción de calor bidimensional y tridimensional. Dicho tipo de conducción de calor multidimensional ocurre dentro del monobloque de una máquina de combustión interna, en el tratamieno de calor de varias partes metalicas, y dentro de cualquier cuerpo compuesto, hecho con materiales que se poseen diferentes conductividades térmicas. Por el momento, limitaremos nuestra discusión bidimensional bajo condiciones de estado estacionario (a saber, la temperatura no varía con el tiempo) sin fuentes de calor. Recuerde, una vez más que el principal objetivo de cualquier análisis de trasferencia de calor es la determinación de la distribución de temperatura y el flujo de...

Leer mas »

Análisis gráfico de conducción de calor bidimensional (I)

Debido a las geometrías irregulares asociadas con problemas específicos y debido a la imposición de ciertas condiciones en la frontera, resulta con frecuencia muy díficil, o imposible, encontrar una solución analítica a los problemas. Muchas veces se puede llegar a una solución aproximada a tráves de medios gráficos. Esto es particularmente cierto si las fronteras del cuerpo en cuestión incluyen segmentos que son isotérmicos. En realidad, para obtener una solución gráfica, quien está resolviendo un problema de este tipo necesita cierta visión, que sólo se consigue a través de una exposición extensiva a problemas de conducción de calor. El trabajo de establecer una solución es alguna "forma de arte", y el estudiante que principia no debe esperar resultados inmediatos de este tipo de enfoque. Para generar una solución gráfica, se crea una red de cuadros curvilineos, dibujando lineas isotermas y de flujo de calor de acuerdo a los lineamientos siguientes: Siempre se dibuj...

Leer mas »

TAbla Algunos valores de conductividades térmicas.

Leer mas »

Ejemplo Calor

Una lola se sirve 1000 Cal en alimentos, los que luego quiere perder levantando pesas de 25 kg hasta una altura de 1.8 m. Calcular el número de veces que debe levantar las pesas para perder la misma cantidad de energía que adquirió en alimentos y el tiempo que debe estar haciendo el ejercicio. Suponga que durante el ejercicio no se pierde energía por fricción. Solución: para perder las 1000 Cal, la lola debe realizar la misma cantidad de trabajo mecánico, es decir W = 1000 Cal. Transformando este valor al SI:

Leer mas »

Transferencia de Calor

Busca en el Sitio

CALOR Y LA PRIMERA LEY DE LA TERMODINAMICA - Problema 9